코딩복습장
선형대수 7강: 벡터의 선형독립과 기저벡터 본문
오늘은 벡터의 선형독립과 기저벡터에 대해 포스팅해보려고 한다.
포스팅 시작~!

강의링크 :
https://www.youtube.com/watch?v=bq3pCPHI4UY&list=PLSN_PltQeOyjDGSghAf92VhdMBeaLZWR3&index=7
강의 노트

교수님께서는 이전강의의 내용을 다시 알려주신다.
변수의 개수가 식의 수보다 많은 경우는 해가 없거나, 해가 무수히 많은 경우이다.
수식의 해를 구하기 위해 우리는 가우스 소거법을 사용한다.
이때 우리는 가우스 소거법을 사용해서 Row Reduced Form으로 matrix를 만들어준다.
이후 pivot에 해당하는 column의 원소를 pivot을 제외하고 모두 0으로 만들어준 뒤에
pivot을 모두 1로 만든다. -> 그러면 관계식이 나오는데
이 관계식을 pivot variable = free variable 형식으로 만들어주고 x를 free variable의 수식으로만 나타내주면
matrix A의 Null Space가 나오게 된다.
그렇다면, b가 0이 아니라면 어떻게 될까?
그러면 Null space가 아니라 A의 해공간이 나오게 된다.
-> 해 공간이 linear space가 아닐수도 있다는 점을 새로 알게 되었다.
(0 벡터를 포함하는 Null Space에서 평행이동 했기 때문에)
affine space라고도 한다.
-> affine space: "선형공간을 어떤 벡터만큼 평행이동시킨 공간"
이때 정답은 우리가 구했던 Null space의 column vector들이 만드는 공간을 실수 vector만큼 평행이동 시킨 space가 된다.
이 실수 vector를 $x_p$라고 하고 Null space를 구성하는 vector를 $x_n$이라고 하면 Row space는 다음과 같이
나타낼 수있다.
$x = x_n + x_p$
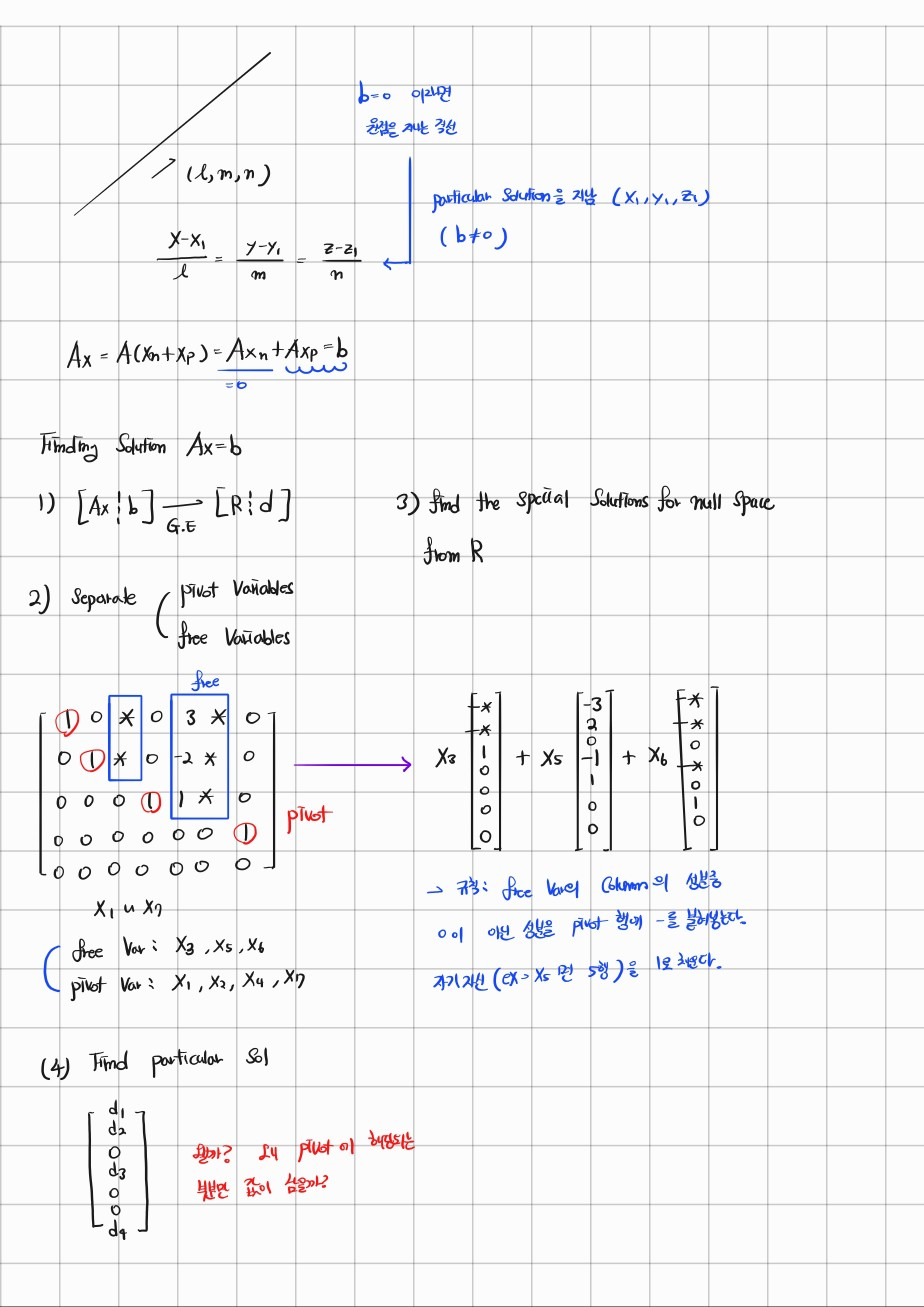
이를 직선으로 비유하자면 원점을 지나는 직선에서 어떤 특정한 particular solution을 지나는 직선으로 바뀌었다고 볼 수 있는 것이다.
정리하자면 수식의 개수와 변수의 개수가 같을때는 G.E를 원래의 방식으로 사용 가능하지만, 수식의 개수보다 변수의 개수가 많을 때는 G.E를 사용하여 matrix를 Row Reduced Form으로 바꿔주어야 한다.

이후 교수님은 Linear Independent에 대해서 설명해주신다.
linear independent란 어떤 Linear combination의 결과가 0이 되기 위해서는 해당 벡터들에 곱해진
스칼라의 값이 모두 0이어야 한다는 조건을 만족시키는 벡터들을 이야기 한다.
그리고 만약 G.E를 적용했을때, m개의 0 벡터가 아닌 row vector가 만들어졌다면 행렬 A는 m개의 independent한 vector를
가지고 있는 것이다.
그리고 independent row vector의 개수는 independent column vector의 개수, A의 rank와 같다.
참고로 G.E를 할때 pivot 위치의 column vector는 independent vector와 같다.

이후 교수님께서는 span에 대해서 설명해주신다.
span은 vector들의 모든 linear combination이 만드는 vector space를 의미한다.
하지만 같은 vector space를 만들더라도 independent vector의 조합에 따라 달라질 수 있다.
Basis는 vector space를 span하는 최소한의 independent vector 이다.
-> 최소한의 독립관계의 벡터를 가지고 vector space를 만들면 linear combination의 결과는 unique해진다.
basis는 여러 조합으로 가능하지만, basis가 결정되면 linear combination의 결과는 유일하다.
마지막으로 교수님은 chapter 3에서는 수식의 개수가 변수의 개수보다 많은 경우를 소개할 것이라고 하며 강의를 마친다.
이상 포스팅 끝~!

'수학 > 선형대수' 카테고리의 다른 글
| 선형대수 6강 : 영벡터 공간과 해집합 (0) | 2025.04.03 |
|---|---|
| 선형대수 5강: 벡터공간과 열벡터공간 (2) | 2025.04.03 |
| 선형대수 4강: 역행렬과 전치행렬 (0) | 2025.04.02 |
| 선형대수 3강 : LU분할 (0) | 2025.04.01 |
| 선형대수2강: 1차 연립방정식과 가우스소거법 (0) | 2025.03.27 |





