코딩복습장
선형대수 3강 : LU분할 본문
오늘은 이상화 교수님의 선형대수 3강을 리뷰해보려고 한다.
강의 링크:
https://www.youtube.com/watch?v=QZk0L7MPDxs&list=PLSN_PltQeOyjDGSghAf92VhdMBeaLZWR3&index=4
강의 노트

우선 교수님께서는 2강에서 소개한 가우스 소거법을 행렬의 곱으로 어떻게 표현할 수 있는지 알려주신다.
이때 각 행렬에 대해 곱해주는 값을 이라고 정의한다.
: 2열의 계수에서 1열의 계수 x 의 값을 뺴준다.
이 과정을 가우스 소거법의 순서에 따라 반복하는 과정을 행렬로 표현하는데, 의 연산을 하는 matrix를
이라고 한다.
위의 예제에서는 총 3번의 소거법을 진행하여 matrix를 Upper triangular형태로 만든다.

그리고 이렇게 만들어진 값에 대해서 ( U: Upper traingular matrix)
$ E_{3, 2} E_{3, 1} E_{2, 1} $ 값만 계산해준다.
그러면 이렇게 만들어진 matrix는 Lower triangular matrix 형태가 된다. (이를 L이라고 표현하자)
그렇다면 행렬 A는 다음과 같이 표시할 수 있다.
이를 LU factorization ( decomposition ) 이라고 한다.
이걸 왜 쓸까..? determinant 계산을 할때 편해서 이 방식을 많이 쓴다고 한다.
그리고 matrix 에 연립의 정보가 모두 담겨있다는 것을 확인할 수 있다.
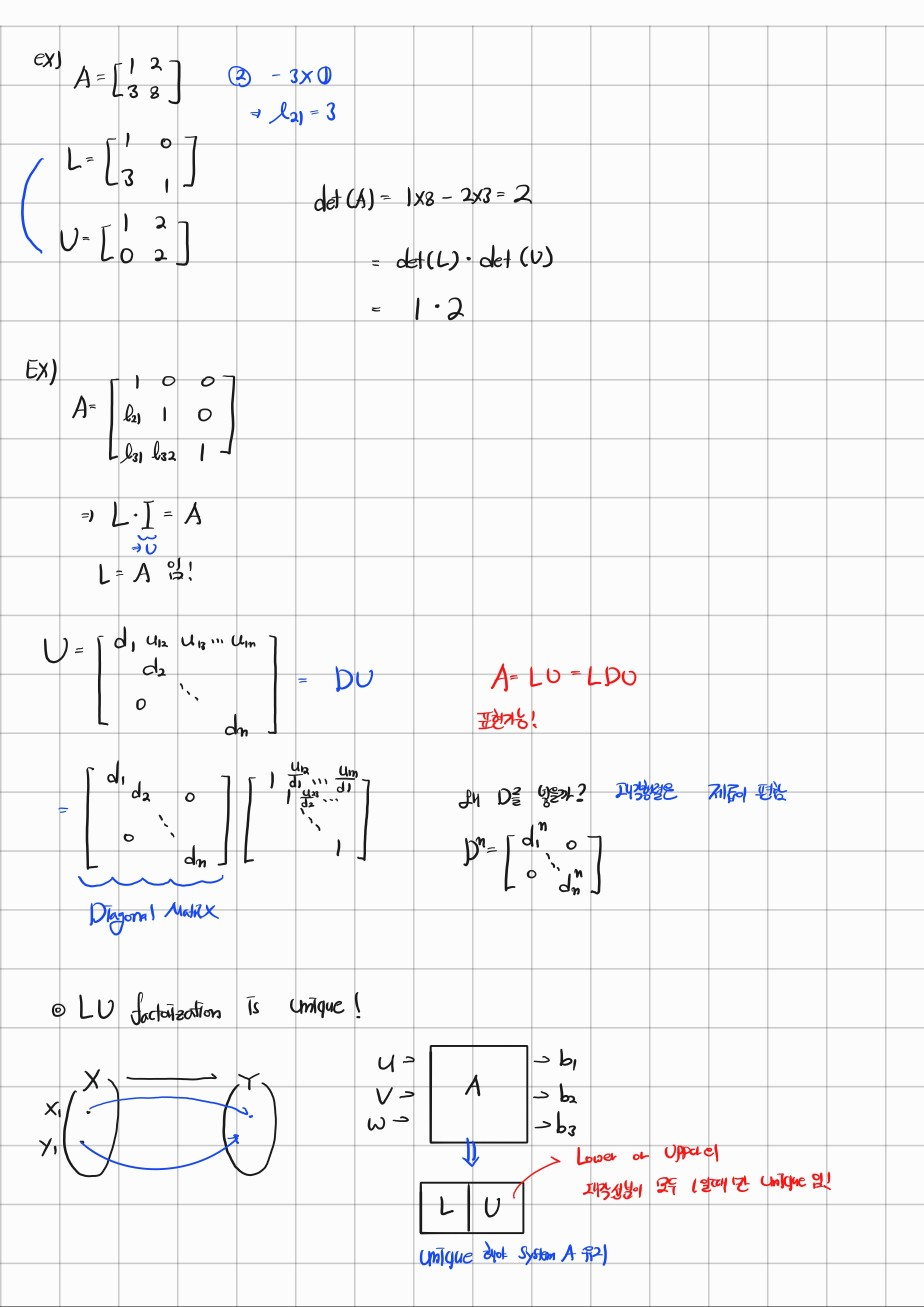
이후에 교수님은 예시를 들어가며 LU 분할에 대해 설명해주셨다.
참고로 초기 matrix A가 Lower triangular matrix라면 U는 identity가 되고 L = A가 된다는 것을 알 수 있다.
그리고 분해된 LU matrix에 대해서 대각행렬을 추가하여 분해할수도 있다.
대각행렬을 추가하는 이유는 제곱연산을 할때 계산하기 편해서라고 한다.
그리고 LU matrix에서 L or U의 대각 성분이 모두 1이라면 L, U matrix는 unique하다고 한다.

우리는 2강에서 가우스 소거법을 배웠을때, pivoting에 대해서도 배웠다.
(Upper triangular 형태가 되지 않을때 행벡터의 순서를 바꾸는 방법)
교수님께서는 pivoting을 하는 과정도 matrix의 곱 관점으로 볼 수 있도록 설명해주셨다.
이렇게 위치를 바꾸는 matrix를 permutation matrix라고 한다.
그리고 이 matrix는 교환법칙이 성립하지 않는다고 한다.
또한 가 성립한다고 한다.
(pivoting이 안된다면 답이 없거나 무한한 경우임)
이상 오늘의 포스팅을 마치겠다.

'수학 > 선형대수' 카테고리의 다른 글
| 선형대수 6강 : 영벡터 공간과 해집합 (0) | 2025.04.03 |
|---|---|
| 선형대수 5강: 벡터공간과 열벡터공간 (2) | 2025.04.03 |
| 선형대수 4강: 역행렬과 전치행렬 (0) | 2025.04.02 |
| 선형대수2강: 1차 연립방정식과 가우스소거법 (0) | 2025.03.27 |
| 선형대수 1강 선형성의 정의, 1차 연립방정식의 의미 (2) | 2025.03.27 |





