코딩복습장
선형대수 4강: 역행렬과 전치행렬 본문
오늘은 선형대수 4강에 대해서 리뷰해보려고 한다.
포스팅 시작!

강의 링크: https://www.youtube.com/watch?v=HPbWCROEFno&list=PLSN_PltQeOyjDGSghAf92VhdMBeaLZWR3&index=4
강의 노트

1. 교수님께서는 역행렬이 있을 조건에 대해서 먼저 설명해주신다.
그리고 역행렬이 있다면 LU로 분할된 matrix에서 U의 대각성분이 모두 non-zero여야 한다는 것을 보여준다.
-> LU로 분할된 matrix의 경우 L, U가 모두 삼각행렬이기 때문에 determinant는 대각성분의 곱임
2. 어떤 matrix 에 대해서 inverse는 unique하다는 것을 증명한다.
3. 만약 이 존재한다면, 의 식의 x나 b 중 하나만 알아도 나머지를 구할 수 있다.
-> 이 invertible 하기 때문
4.
이 식에서 만약 b = 0이라면 x=0 으로 trivial solution이라고 한다.
(trivial solution이란 자명한 해라는 뜻으로 해가 x=0하나로만 정해진다는 뜻이다. )
이 존재하지 않으면 non-trivial solution일 수 있다. (해가 하나가 아닐 수 있다라는 뜻)
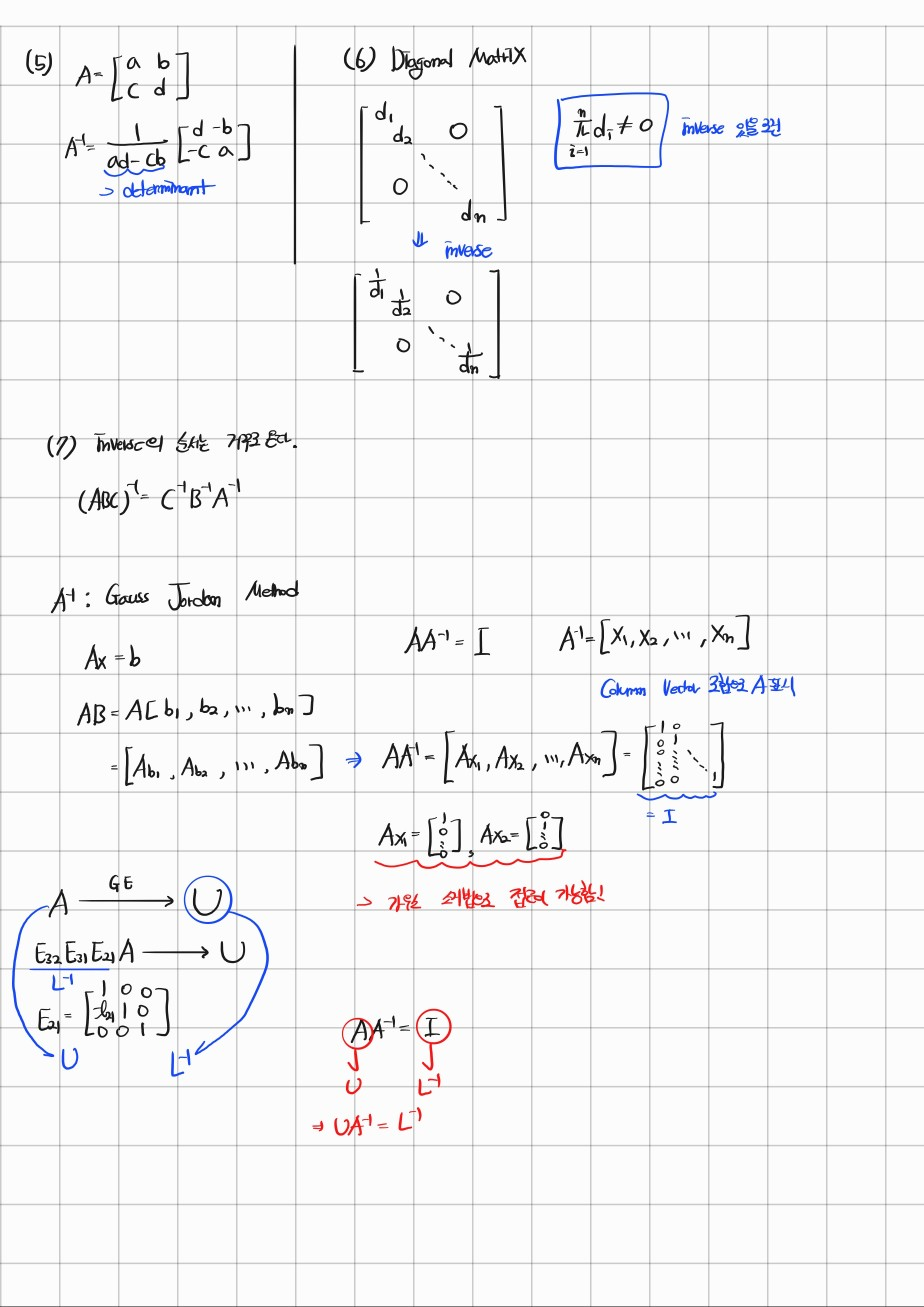
5. 2x2행렬에서 determinant를 구하는 방법
6. diagonal matrix의 inverse를 구하는 방법
7. inverse시킨 것의 행렬곱 순서는 반대이다.
이후 교수님은 가우스 조던 소거법을 소개해주신다.
가우스 조던 소거법은 행렬을 단위행렬(대각성분을 모두 1로 만들고 나머지를 0인 matrix)로 만드는 방법이다.
선형방정식의 해를 구하기 위해 사용되는 방법이다.
교수님께서는 이 방법을 가우스 소거법이랑 연관지어 설명하신다.
이 식에서 을 column vector로 이루어진 matrix로 본다. ->
이때 에서 A에 Gauss 소거법을 적용하면 이 된다.
교수님의 위의 예시를 들어주신다.
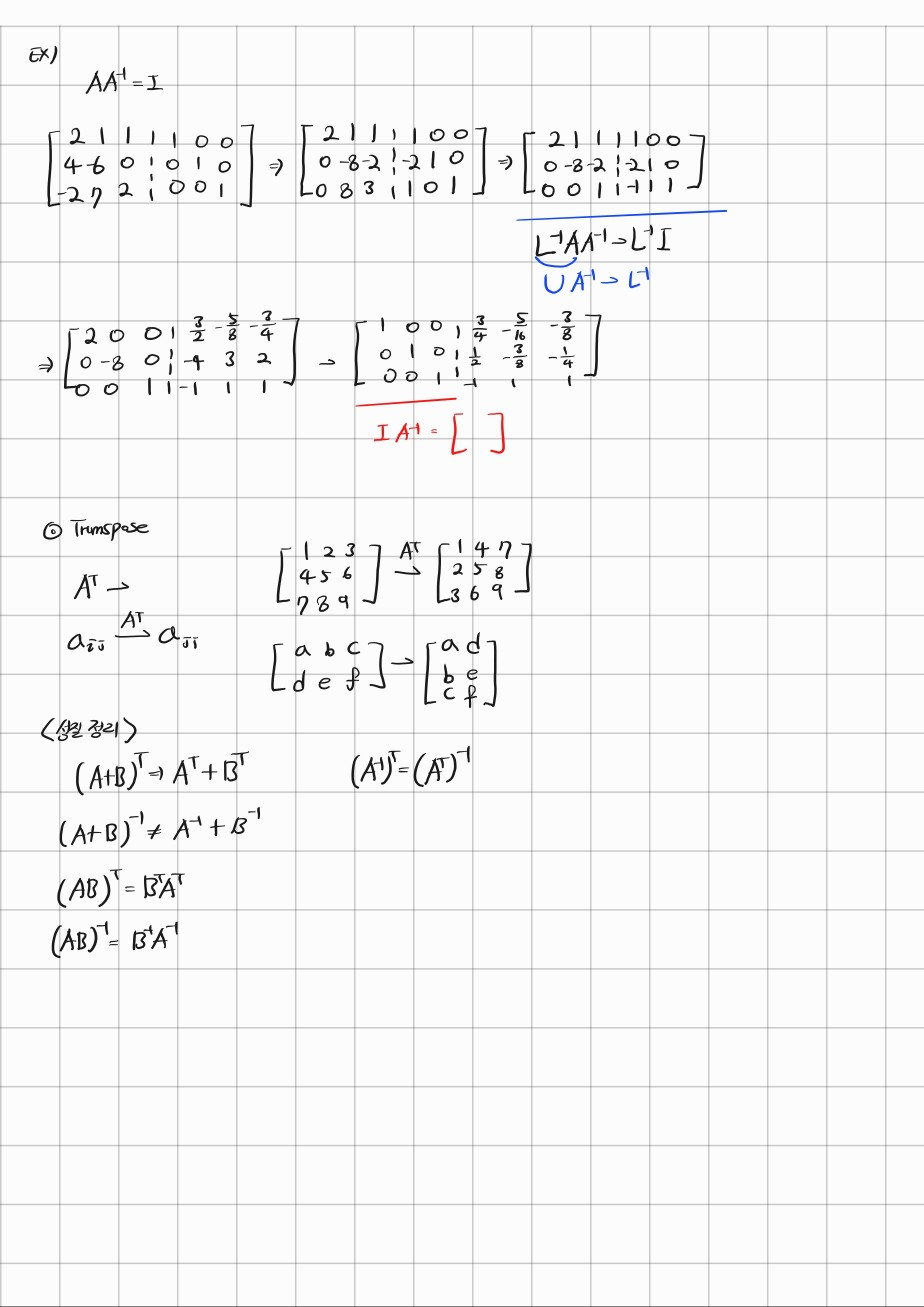
결국 을 미지수로 놓은 상태에서 를 좌변에 곱해주는 것이다.
-> 이 과정이 계수를 Identity로 만듬(단위행렬) -> 가우스 조던 소거법 완료
이 되는 것이다.
다음은 transpose에 대해서 설명해주신다.
Transpose는 덧셈에서 분배법칙이 가능하고, 곱해진 식에 대해서 transpose를 적용하면 순서가 바뀌며 적용된다.
그리고 inverse와 T는 순서가 바뀌어도 상관이 없다.
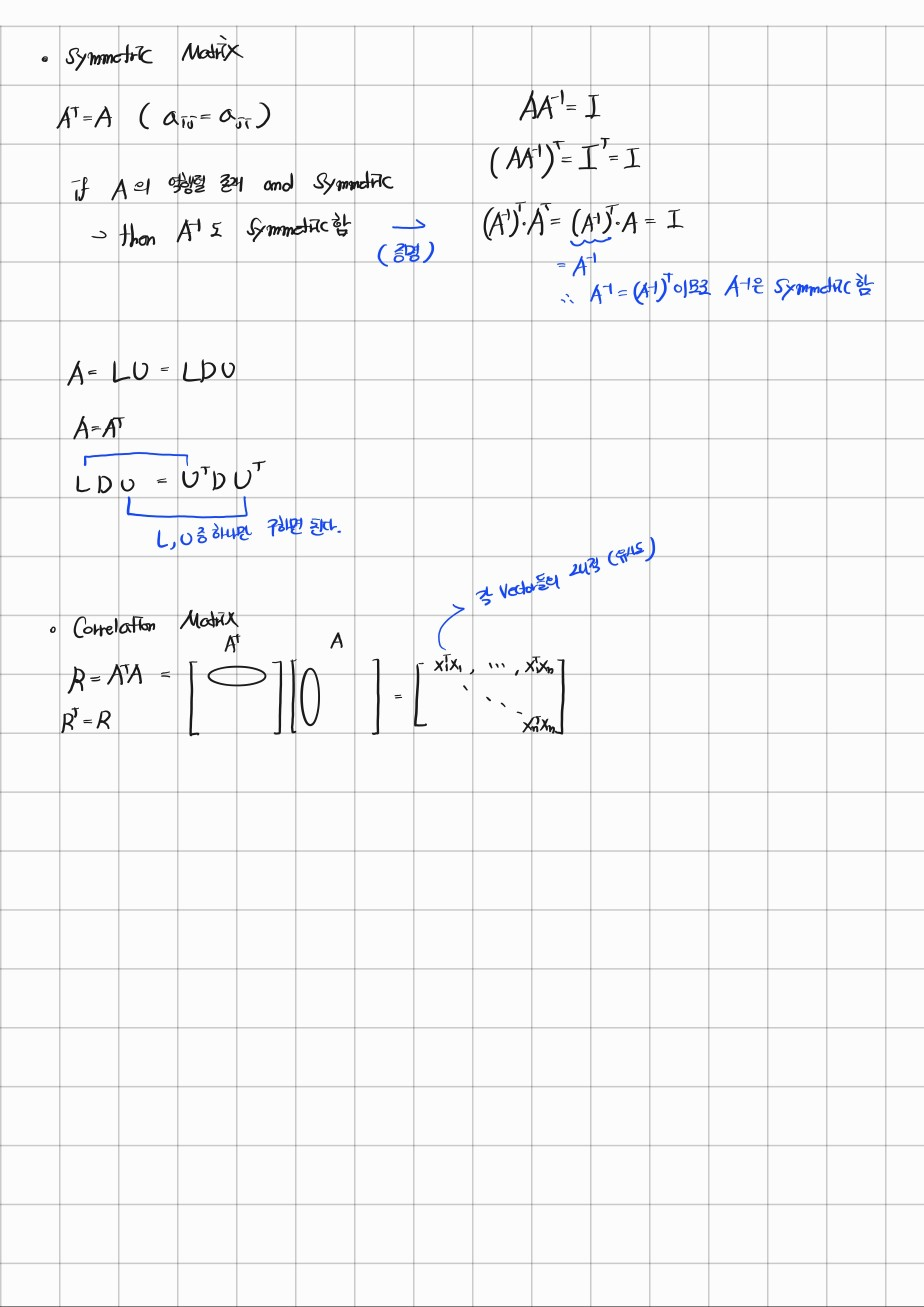
다음은 symmetric matrix에 대해서 설명한다.
가 symmetric하면 도 symmetric하다.
그리고 교수님께서는 Correlation matrix에 대해서 설명해주신다.
는 각 벡터의 내적으로 성분이 구성되므로 벡터간의 유사도로 사용할 수 있어 correlation이 된다고 한다.
이상 오늘의 포스팅 끝!

'수학 > 선형대수' 카테고리의 다른 글
| 선형대수 6강 : 영벡터 공간과 해집합 (0) | 2025.04.03 |
|---|---|
| 선형대수 5강: 벡터공간과 열벡터공간 (2) | 2025.04.03 |
| 선형대수 3강 : LU분할 (0) | 2025.04.01 |
| 선형대수2강: 1차 연립방정식과 가우스소거법 (0) | 2025.03.27 |
| 선형대수 1강 선형성의 정의, 1차 연립방정식의 의미 (2) | 2025.03.27 |





