코딩복습장
선형대수 1강 선형성의 정의, 1차 연립방정식의 의미 본문
선형대수 지식의 부족함을 느껴 이상화 교수님의 선형대수 강의를 듣게 되었다.
강의 링크는 아래에서 확인할 수 있다.
https://www.youtube.com/watch?v=i3VTeQW0Tw4&list=PLSN_PltQeOyjDGSghAf92VhdMBeaLZWR3&index=2
강의 필기 정리본

먼저 Linearity의 개념에 대해서 설명해주신다.
핵심은 Linearity는 Superposition과 Homogeniety를 만족할 때 성립한다는 것이다.
Linearity는 미분과 적분, 행렬 모두에 적용이 된다.

다음으로는 행렬 계산의 표기 방법에 대해 설명한다.
Linear Combination 계산의 편의를 위해 Column vector를 기본으로 계산한다는 말과 Transpose, 행렬의 사칙연산에 대해 설명한다.
함수의 내적을 vector관점으로 소개하고 수식으로 간단하게 정리한 후 이를 힐베르트 공간이라고 소개해주신다.
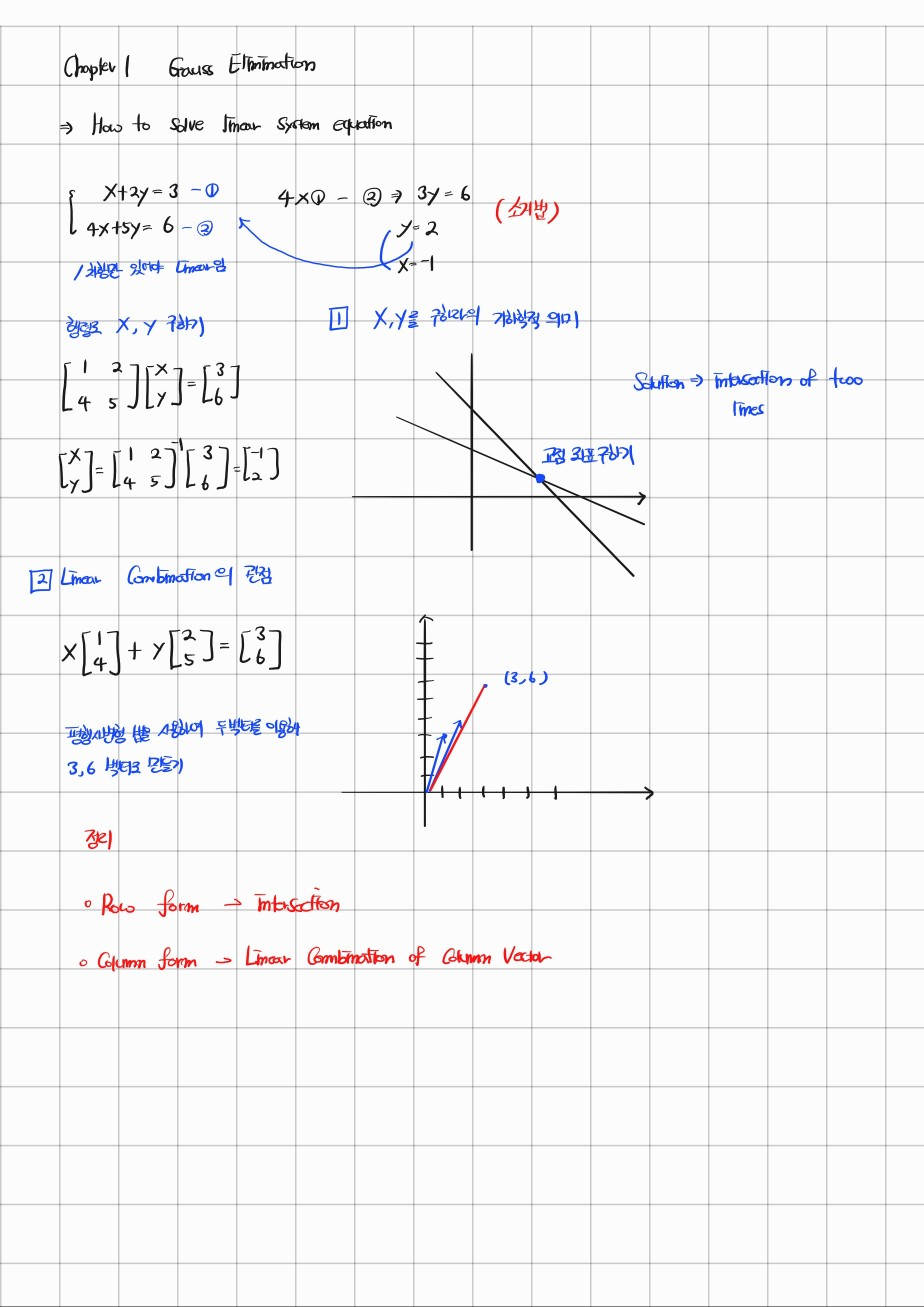
연립방정식이 주어진 상황에서 관점을 어떻게 보는지에 따라 해석이 달라진다는 점을 간단 명료하게 설명해주신다.
- Row의 방향으로 봤을 때
고등학교를 다닐 때 배웠던 소거법을 사용하여 계산한다.
-> x, y에 대한 해석은 직선의 교점이다. (3차원이면 평면의 intersection)
- Column의 방향으로 봤을 때
Linear Combination을 사용하여 계산한다.
-> 계수를 Column vector로 사용하고 x, y를 잘 조절하여 평행사변형 법으로 결과값 벡터를 만들어내는 방식
이번 강의를 들으면서 계산 방식에 따라 결과를 구하는 과정에 대한 관점이 바뀔 수 있다는 점이 인상깊었다.
Linearity가 필요한 이유
| 💡 단순성 | 계산, 해석, 구현이 쉬움 |
| 🧩 조립 가능 | 여러 입력을 합성해 전체 결과 예측 가능 ( superposition ) |
| 🧠 직관성 | 기하적으로 해석 가능 (회전, 확대 등) |
| 🔄 근사 가능 | 비선형도 국소적 선형 근사 가능 ( 테일러 급수, back propagation |
'수학 > 선형대수' 카테고리의 다른 글
| 선형대수 6강 : 영벡터 공간과 해집합 (0) | 2025.04.03 |
|---|---|
| 선형대수 5강: 벡터공간과 열벡터공간 (2) | 2025.04.03 |
| 선형대수 4강: 역행렬과 전치행렬 (0) | 2025.04.02 |
| 선형대수 3강 : LU분할 (0) | 2025.04.01 |
| 선형대수2강: 1차 연립방정식과 가우스소거법 (0) | 2025.03.27 |





