코딩복습장
그리디 알고리즘 예제2: 큰 수의 법칙 본문
문제
동빈이의 큰 수의 법칙은 다양한 수로 이루어진 배열이 있을 때 주어진 수들을 M번 더하여 가장 큰 수를 만드는 법칙이다. 단, 배열의 특정한 인덱스(번호)에 해당하는 수가 연속해서 K번을 초과하여 더해질 수 없다.
예를 들어 순서대로 2, 4, 5, 4, 6으로 이루어진 배열이 있을 때 M이 8이고, K가 3이라고 가정한다. 예를 들어 순선대로 2, 4, 5, 6으로 이루어진 배열이 있을 때 M이 8이고, K가 3이라고 가정하자. 이 경우 특정한 인덱스의 수가 연속해서 세번까지만 더해질 수 있으므로 큰 수의 법칙에 따른 결과는 6 + 6 + 6 + 5 + 6 + 6 +6 +5인 46이 된다.
단, 서로 다른 인덱스에 해당하는 수가 같은 경우에도 서로 다른 것으로 간주한다. 예를 들어 순서대로 3, 4, 3, 4, 3으로 이루어진 배열이 있을 때 M이 7이고, K가 2라고 가정하자. 이 경우 두 번째 원소에 해당하는 4와 네 번째 원소에 해당하는 4를 번갈아 두 번씩 더하는 것이가능하다. 결과적으로 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4인 28이 도출된다.
배열의 크기 N, 숫자가 더해지는 횟수 M, 그리고 K가 주어질 때 동빈이의 큰 수의 법칙에 따른 결과를 출력하시오.
입력 조건
1. 첫째 줄에 N(2 <= N <= 1,000), M(1 <= M <= 10,000), K(1 <= K <= 10,000)의 자연수가 주어지며, 각 자연수는 공백으로 구분한다.
2. 둘째 줄에 N개의 자연수가 주어진다. 각 자연수는 공백으로 구분한다. 단, 각각의 자연수는 1 이상 10,000 이하의 수로 주어진다.
3. 입력으로 주어지는 K는 항상 M보다 작거나 같다.
출력 조건
첫째 줄에 동빈이의 큰 수의 법칙에 따라 더해진 답을 출력한다.
입력 예시
5 8 3
2 4 5 4 6
출력 예시
46
나의 풀이
나는 이 문제를 봤을 때 가장 큰 숫자를 k번 만큼 연속으로 사용하고 다른 숫자로 한번 끊으면 다시 k번 연속해서 사용할 수 있다는 점을 먼저 생각했다.
그러면 문제의 정답은
가장 큰 수 * k + 두 번째로 큰 수
를 반복하여 작성하는데, 길이 m을 만족시키는 배열을 만들면 된다.
나는 이때 가장 큰 수와 두 번째로 큰 수를 구하는 방법을 배열의 전체 구간을 정렬시키는 방법 대신에
max heap을 두 번 사용하는 방법을 쓰고 싶었다.
그렇게 된다면 이 과정의 시간복잡도는 O(nlogn) -> O(logn)이 될 것이다.
이후 그렇게 구한 두 값을 위의 패턴으로 합하는 방식을 사용해서 정답을 구했다.
패턴에 따라 m개의 배열을 생성하는 과정은 m번 반복하기 때문에 시간복잡도는 O(m + log n)이 될 것이다.
작성한 코드
n, m, k = map(int, input().split())
data = list(map(int, input().split()))
def heapify(arr_len, arr): # max heap 구현
last_parent = arr_len//2 - 1 # 가장 마지막 순서의 parent
for current in range(last_parent, -1, -1): # current node를 last_parent부터 놓고 탐색
while current <= last_parent: # current가 leaf node가 아닌지 check
child = current*2 +1 # parent의 왼쪽 child
sibling = child + 1 # parent의 오른쪽 child
if sibling < arr_len and arr[sibling] > arr[child]: # array 길이 안에 있고 오른쪽 child가 왼쪽보다 큰 경우
child = sibling # child 값을 더 큰 값으로 바꿈
if arr[current] < arr[child]: # child가 부모 node인 current보다 클 때
arr[current], arr[child] = arr[child], arr[current] # 두 값을 바꿔준다.
current = child # 바꿔진 부모노드의 data 위치가 맞는지 확인해야 한다. -> current를 바뀐 부모 노드 데이터 위치로 바꿔줌
else:
break
def maximum_sum(m, k, first_num, second_num): # 연속된 숫자를 허용한 최대 합 구하기
sum = 0 # 합의 결과
temp = 0 # 현재 연속된 숫자의 개수
curr_length = 0 # 현재 배열의 길이
while curr_length < m: # 배열의 길이는 m을 넘을 수 없음 (제약조건)
if temp < k: # 연속된 숫자의 길이 제한
sum += first_num
temp += 1
else: # 연속된 숫자가 k보다 많기 때문에 두번째 큰 숫자로 연속된 숫자를 초기화 시켜줌
sum += second_num
temp = 0 # 연속 숫자 초기화
curr_length += 1
return sum # 결과 값 반환
def maximum_arr(arr, n, m, k):
for length in range(len(arr), len(arr)-2, -1): # 전체 배열을 sort하기 보다 두번만 max heap을 구하는 것을 선택
heapify(length, arr)
arr[0], arr[length-1] = arr[length-1], arr[0]
print(arr)
first_num = arr[n-1]
second_num = arr[n-2]
print(first_num)
print(second_num)
res = maximum_sum(m, k, first_num, second_num)
return res
result = maximum_arr(data, n, m, k)
print('가장 큰 수는 {} 입니다.'.format(result))
실행결과
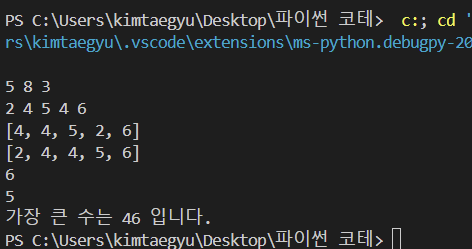
max heap을 라이브러리 없이 만들었기 때문에 정답코드보다 코드의 길이가 좀 길었다.
정답코드
n, m, k = map(int, input().split(' '))
data = list(map(int, input().split(' ')))
data.sort()
first = data[-1]
second = data[-2]
result = 0
while True:
for i in range(k):
if m == 0: # m이 0이라면 반복문 탈출
break
result += first
m -= 1
if m == 0:
break
result += second
m -= 1
print(result)
패턴을 사용하여 더하는 코드 부분에서 정답코드가 더 깔끔하게 잘 작성한 것 같다.
아직 좀 부족하구만..

그래도 정답코드보다 시간복잡도면에서는 훌륭하게 작성했다.
포스팅 끝~!
'코딩 테스트 > 파이썬 알고리즘 기초' 카테고리의 다른 글
| 그리디 알고리즘 예제4: 1이 될 때까지 (0) | 2025.04.06 |
|---|---|
| 그리디 알고리즘 예제3: 숫자카드 게임 (0) | 2025.04.06 |
| 그리디 알고리즘 예제1: 거스름돈 (2) | 2025.04.06 |


