PCA 구현(파이썬)

오늘은 PCA를 구현해보는 실습을 하려고 한다. 

 

https://towardsdatascience.com/a-step-by-step-implementation-of-principal-component-analysis-5520cc6cd598/

A Step By Step Implementation of Principal Component Analysis | Towards Data Science

 

실습에 사용한 코드는 위의 링크에서 확인할 수 있다. 

 

 

시각화 코드는 따로 주어지지 않았기 때문에 직접 작성해야했다.

 

 실습 Colab 링크:

https://colab.research.google.com/drive/1g7PJtDdescIVoocs0R8cxgzNogpWfIMw?usp=sharing

2025-1 PCA실습.ipynb

 

# Create random 2d data
mu      = np.array([10, 13])
sigma   = np.array([[3.5, -1.8],
                    [-1.8, 3.5]])

print("Mu ",    mu.shape)
print("Sigma ", sigma.shape)

# Create 1000 samples using mean and sigma
org_data = rnd.multivariate_normal(mu, sigma, size=(1000))
print("Data shape ", org_data.shape)

 

나는 우선 정해진 평균과 공부산을 사용하여 normal 분포에서 sample을 100개 뽑았다. 

 

 

그래프는 다음과 같은 모양으로 나온다.

 

# Subtract mean from data
mean = np.mean(org_data, axis= 0)
print("Mean ", mean.shape)
mean_data = org_data - mean
print("Data after subtracting mean ", org_data.shape, "\n")

 

이후에 sample들의 평균을 원점으로 바꾸기 위해 모든 sample에서 평균을 뺴준다. 

 

공분산을 matrix의 곱셈으로 구하고 싶었기 때문

 

이후 중심을 옮긴 데이터와 원본 데이터를 시각화했다. 

 

 

중심이 잘 이동된 것을 확인할 수 있었다. 

 

# Compute covariance matrix
cov = np.cov(mean_data.T)
# cov = np.round(cov, 2)
print("Covariance matrix ", cov.shape, "\n")
print(cov)

 

이후에 cov함수로 covariance matrix를 구한다. 

 

구하는 방식은 데이터 sample들의 내적으로 구할 수 있다. 

 

Transpose를 하고 넣어준 이유는 sample의 데이터 값이 row축으로 가야 함수가 공분산을 구해주기 때문이다. 

 

나는 왜 공분산을 구할 때 자기자신을 내적하는지도 궁금해졌다. 

 

 

자기자신의 내적을 하면 자신의 matrix를 column vector들로 봤을때 결과 행렬의 원소를 column vector들의 내적이라고

볼 수 있다. 

 

따라서 데이터를  x, y좌표라고 했을때 x, y 사이의 관계를 구할 수 있다는 것이다. 

-> 내적을 함으로써 유사도를 구할 수 있음 -> 음수면 반비례, 양수면 비례 관계임 

 

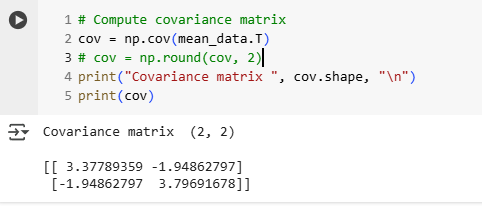
구한 x, y의 관계가 음수가 나왔기 때문에 x, y는 반비례함을 확인할 수 있고 실제로 그래프도 음수 기울기 방향으로 

그려지는 것을 확인할 수가 있다.

 

그리고 벡터의 내적은 스칼라이기 때문에 xy, yx내적은 같은 값이다. 따라서 공분산 matrix는 symmetric하다는 것을 

확인할 수도 있다. 

 

# Perform eigen decomposition of covariance matrix
eig_val, eig_vec = np.linalg.eig(cov)
print("Eigen vectors\n", eig_vec)
print("Eigen values\n", eig_val, "\n")

 

이후에 나는 eigen value와 eigen vector를 구해주었다. (사용한 함수는 eig함수이다. )

 

축이 2개이기 때문에 eigen value는 2개의 값이 나온다. 

 

 

# Sort eigen values and corresponding eigen vectors in descending order
indices = np.arange(0, len(eig_val), 1)
indices = ([x for _, x in sorted(zip(eig_val, indices))])[::-1]     # can also use argsort()[::-1]
eig_val = eig_val[indices]
eig_vec = eig_vec[:, indices]
print("Sorted Eigen vectors ", eig_vec)
print("Sorted Eigen values ", eig_val, "\n")

 

이후 나는 eigen value의 크기에 따라 eigen value, eigen vector들을 내림차순으로 정렬시켜주었다. 

 

1. 정렬시키는 과정은 다음과 같다. 
2. arange로 index list를 만든다. 
3. zip으로 eigen value와 index를 묶는다. 
4. eigen vector로 sort(오름차순)한 이후 index만 뽑아 list를 만든다. 
5. [::-1]을 사용하여 내림차순으로 만든다. 
6. 만든 index를 사용하여 eigen value, eigen vector들을 내림차순으로 정렬시킨다. 

정렬이 잘 된 것을 확인할 수 있다. 

 

# Get explained variance
sum_eig_val = np.sum(eig_val)
explained_variance = eig_val / sum_eig_val
print(explained_variance)
cumulative_variance = np.cumsum(explained_variance)
print(cumulative_variance)

 

이후에 벡터의 축을 어느정도 사용하면 얼마나 설명가능한지 (원본 데이터가 유지되는지) 정도를 구해보았다. 

 

설명가능한 정도는 전체 eigen value의 합으로 eigen value matrix를 나눠서 구할 수 있다. 

 

 

가장 큰 eigen value만 사용하면 77%정도 데이터를 설명 가능하고, 두 번째는 22% 설명가능하다. 

 

cumulative sum을 사용하여 matrix를 보고 얼마나 압축할지 보통 결정한다고 한다. 

 

두개를 다 사용했다면 데이터의 축을 전부 사용한 것이기 때문에 설명가능도가 1인 것을 확인할 수 있다. 

 

나는 모든 축을 사용해서 데이터를 projection 시킬 것이다. 

# Take transpose of eigen vectors with data
pca_data = np.dot(mean_data, eig_vec)
print("Transformed data ", pca_data.shape)

 

다음과 같이 eigen vector를 사용하여 데이터들을 선형변환 시켜주었다. 

 

그리고 그래프를 뽑아보았다. 

 

 

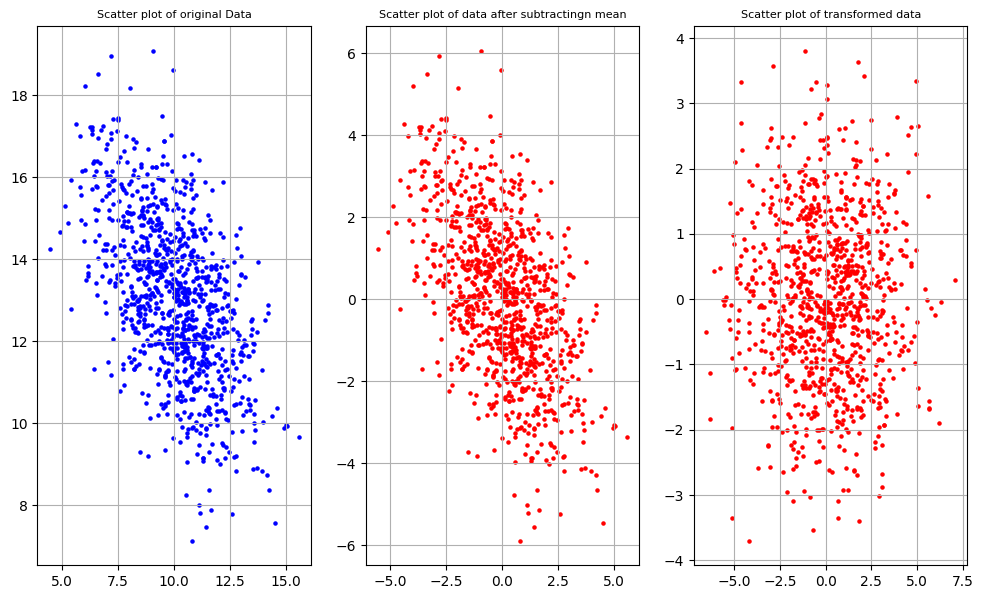
첫 번째는 오리지날 데이터, 두 번째는 평균이 원점인 데이터, 세 번째는 projection한 데이터이다. 

 

projectio을 했을 때, eigen vector가 x, y축이 된다는 것을 확인할 수 있다. 

 

측 eigen vector에 따라 sample들이 정렬이 되는 것이다. 

 

이후에 projection한 이 데이터들을 복원할 것인데 이 과정을 reconstruction 이라고 한다. 

 

- When matrix $\mathbf{P}$ is orthogonal matrix then $\mathbf{P}^{-1} = \mathbf{P^T}$.
- Projection(Transformation): $\mathbf{Y} = \mathbf{X}\mathbf{P}$
- Reconstruction: $\mathbf{Y}\mathbf{P}^{-1}=\mathbf{X}\mathbf{P}\mathbf{P}^{-1}=\mathbf{X}\mathbf{I}$

 

orthogonal matrix의 inverse와 transpose는 같다고 볼 수 있다. 

 

왜 그렇냐면 othogonal matrix의 column vector들은 서로 수직이기 때문이다. 

 

따라서 Transpose로 내적을 하면 column vector들은 자기 자신과의 내적을 제외하면 다른 원소와 내적한 것이

전부 0이 나온다.

 

 

우리는 eigen value를 통해 eigen vector값을 조정할 수 있는데 자기 자신의 column vector내적을 1이 되도록 만들면 

Transpose 행렬과 내적이 identity matrix가 되도록 조정할 수 있는 것이다. 

 

eigen vector는 orthogonal matrix이기 때문에 위의 법칙이 성립한다. 

 

PinvP = np.linalg.inv(eig_vec) @ eig_vec
PtrsP = eig_vec.T @ eig_vec

print('P-inv @ P:\n', np.round(PinvP, 2))
print('P-transpose @ P\n', np.round(PtrsP, 2))

 

나는 이 과정을 실제로 확인해보았다. 

두 값이 같다는 것을 확인할 수 있었다. 

 

따라서 우리는 projection한 데이터 Y에 $X^T$를 곱하고 평균을 더해주면 원래의 데이터로 복원이 가능한 것이다. 

 

recon_data = pca_data.dot(eig_vec.T) + mean
print(recon_data.shape)

 

그려본 그래프는 원본과 똑같은 것을 확인할 수 있다. 

 

모든 축을 다 사용했기 때문에 원본과 같은 것이다. 

 

한가지만 사용한다면 원본과 비슷하지만 다른 데이터로 복원이 되었을 것이다. 

 

이상 포스팅 끝~!