MLE, MAP

이번 글은 머신러닝의 기초인 MLE, MAP에 대해서 정리하려고 한다. 

 

🔹 Probability(확률)와 Likelihood(가능도)

 

확률은 무엇일까?

 

확률은 주어진 확률분포에서 관측값이 나올 확률이다.

X가 확률을 구하고 싶은 사건이라고 하고, D가 주어진 확률분포라고 하자

수식은 다음과 같다.

 

 

 

likelihood는 어떤 사건이 일어났을때, 그 사건이 특정 분포에서 일어났을지에 대한 확률이다. 

D는 정해지지 않은 확률분포이고 하고, X가 관측된 값이라고 하자

수식은 다음과 같다.

 

 

즉, 확률의 개념과는 반대로 주어진 관측값으로 해당 사건이 어떤 확률 분포에서 왔는지를 추정하는 것이다.

 

---

 

🔹 MLE (Maximum Likelihood Estimation) 

 

MLE란 각 관측값 X에 대한 모든 Likelihood의 곱이 최대가 되도록 하는 확률 분포를 찾는 것이다. 

• $\theta$: 사건에 대한 확률 값
• $X$: 사건들
• $x_i$: $i$번째 사건

$L(\theta|Data) = P(Data|\theta)$ 로 계산할 수 있다. 

 

이렇게 구한 $\theta$에 log를 취해주자 (확률은 곱하면 곱할수록 0으로 가기때문)

이후 $P(X|\theta)$를 관측된 각 사건에 대한 확률의 곱으로 변경해준다. (각 사건은 mutually exclusive)

* mutually exclusive: 이벤트 또는 사건이 발생하게 되면 다른 이벤트는 발생하지 않는다는 것

 

$\theta$가 주어졌을때, data가 관측될 확률을 최대화시키는 $\theta$를 $\theta_{MLE}$라고 한다.

 

여기서 중요한 점은 MLE 추정시, 먼저 임의의 확률 분포를 가정해야 한다는 점이다. 

 

왜 그럴까?

 

만약 확률분포를 가정하지 않은 상태로 단순하게 관측되는 데이터만을 보게 되면 측정된 데이터들은 단순히 

데이터 point로만 존재하게 될 것이다. 따라서 관측된 값을 이용해서 데이터들의 패턴을 일반화시키기 위해 

확률분포를 가정해야 한다고 생각한다. 

 

예시를 들기 위해 관측된 데이터의 분포가 정규분포에서 온다고 생각해보자

 

붉은점들이 관측된 데이터들이다. 

 

 

우리는 관측된 값들이 어떤 분포에서 왔는지는 정확히 모른다. 

 

따라서 우리는 likelihood를 사용하여 이 데이터들이 어떤 확률분포에서 왔을 확률이 높은 지에 대해 알아봐야한다. 

 

아래 사진은 관측된 데이터들을 사용하여 만들어낸 likelihood들이다. 

 

 

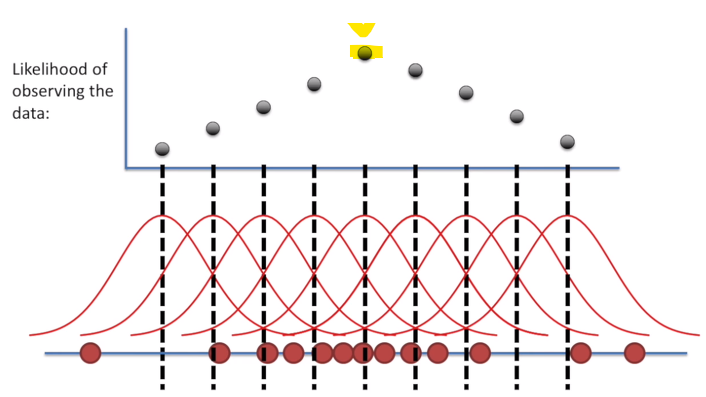
이 그림을 통해 추정된 분포에서 관측값이 나왔확률이 가장 높은 분포는 likelihood가 가장 높은 분포( 노란색 )

이라고 추정할 수 있다. 

 

이 개념을 머신러닝에 적용을 해보자.

 

우리는 model을 사용해서 관측을 한다. -> 관측값을 사용하여 다른 input이 들어갔을때의 output을 구한다. 

 

이는 모델 자체가 관측값이 나왔을 확률분포가 되도록 만드는 것이라고 해석할 수 있을 것 같다. 

 

 

MLE의 문제점

 

MLE는 관측된 데이터만으로 확률분포를 추정하기 때문에 우리가 사전에 알고있는 지식을 반영하지 않는다.

 

주사위로 예시를 들어보자.

 

주사위를 6번 던졌지만 1이 한번도 나오지 않은 상황이라고 가정했을때, MLE는 1이 나올 확률값이 0에 가까운 분포가

나올 것이다. 하지만 실제로는 모두 같은 값이 나오는 uniform 분포이다.

 

이처럼 MLE는 우리가 가지고 있는 사전지식을 반영하지 않는다는 문제가 있다. 

 

그렇다면 사전지식을 반영하는 방식은 없을까?

---

🔹 MAP (Maximum a Posteriori Estimation)

MAP는 내가  알고있는 사전지식을 반영하여 Posteriori Probability가 최대가 되도록 하는 방법이다.

 

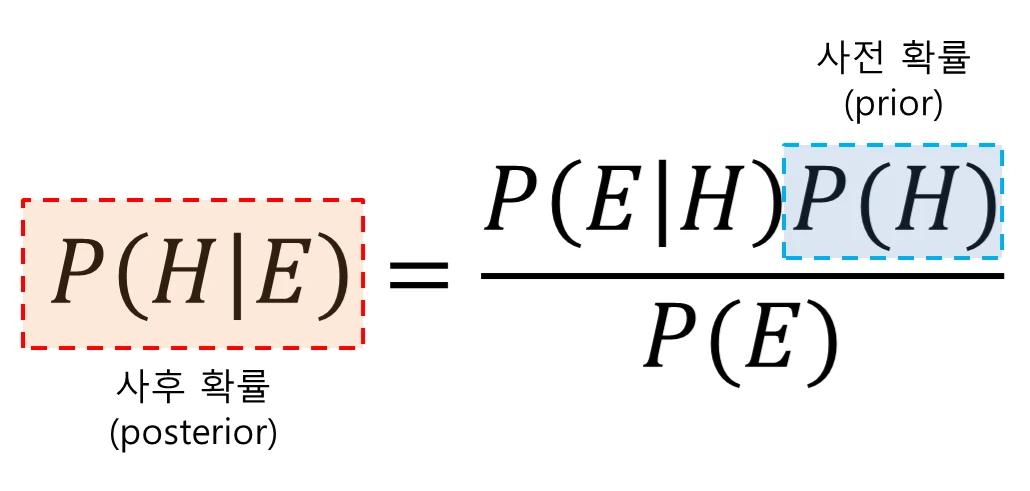
그래서 이게 왜 필요할까?

 

동전던지기의 수행횟수가 충분하지 않은 경우를 예시로 들어보자

 

동전을 두 번 던졌는데, 두 번 전부 앞면이 나온 경우 -> 이때 MLE의 값은 앞면이 나올 확률이 1인 경우가 될 것이다. 

(물론 확률분포는 베르누이 분포라고 가정)

 

하지만 이 분포는 틀렸다. -> 이것이 MLE의 단점

 

우리는 사건의 관측횟수가 부족한 경우에 사전지식을 활용하여 MLE예측을 보완할 수 있는데 그 방법이 바로 베이즈 정리를 이용한 MAP인 것이다. 

 

수식을 살펴보자.

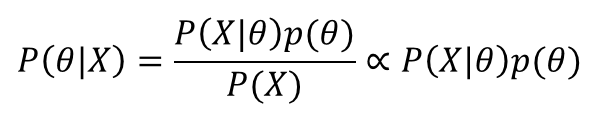
$P(x)$는 사건이 발생한 확률이기 때문에 상수이다. -> 비례식에서는 생략 가능 

 

 

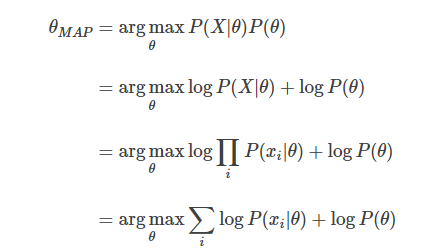
MLE의 방식과 같은 방식으로 log를 취한 후 수식을 정리하면 MAP의 수식이 나온다.

 

---

 

그렇다면 MLE와 MAP가 같아지는 상황은 언제인가?

 

주어진 상황은 동전던지기 상황이다. ($a_H$: 동전 앞, $a_T$: 동전 뒤)

 

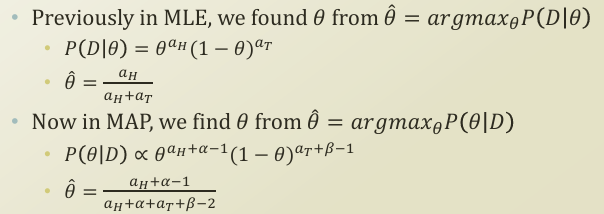
이때 사전에 알고있는 확률인 $P(\theta)$는 알파, 베타로 구성된 분포에서 나온다고 가정했을때

 

시행횟수가 많아진다면 알파, 베타의 값보다 시행횟수의 값이 상대적으로 커져 MLE와 MAP가 거의 동일한 값을 

가진다고 한다. 

 

-> 시행횟수가 많아지면 비슷한 값을 가짐