| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 아니메컵
- 27448
- C
- 딥러닝
- lgb
- 샤논 엔트로피
- ps
- 코복장
- dp
- python
- 모두의 꿈
- dfs
- 스펨메일 분류
- 다이나믹 프로그래밍
- 파이썬
- 2247
- 실질적 약수
- 코테
- 백준
- 코딩테스트
- 힙 정렬
- 17070
- 코딩
- 구현
- T tree
- 정렬
- 부분수열의 합2
- 정답코드
- BFS
- populating next right pointers in each node
- Today
- Total
코딩복습장
Xgboost 본문
xgboost는 Extreme Gradient Boost의 준말이며 그 정의는 다음과 같다.
xgboost는 기존 gradient tree boosting 알고리즘에 과적합 방지를 위한 기법이 추가된 지도학습
알고리즘이다.
xgboost는 base learner를 decision tree로 하며 gbm과 같이 residual을 이용하여 이전 모형의 약점을
보완하는 방식으로 학습한다.
xgboost는 과적합 방지를 위한 파라미터가 추가되어 있다.
XGBoost 알고리즘
먼저 데이터 $(x_i, y_i)$가 있다고 해보자.
그리고 2차 미분이 가능한 손실함수 L이 있다고 하자.
개별 모형의 최대 개수를 M, 학습률 l, 그리고 파라미터 $/gamma, /lambda$를 설정한다.
XGBoost 알고리즘은 다음과 같다.
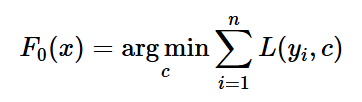
1. 초기 모형은 상수로 설정하여 다음과 같이 찾는다.
Loss function으로 label과 상수 c를 비교하여 오차의 평균이 가장 작은 상수 c를 초기 모형으로 선택한다
2. m = 1, ..., M에 대해서 다음의 과정을 반복한다.

일단 $x_i$에 대한 예측된 k+1 번째 label값은 $F_k(x_i)$ + (l x $/phi(x_i)$)가 된다.
l은 learning rate임.
이렇게 예측한 값과 label의 오차를 구하고 loss를 미분하여 최적의 분할지점에 대한 정보를 찾아야 한다.
이 과정에서 Taylor Expansion이 사용된다.
직접 미분을 하지 않는 이유는 $/phi$함수 때문이다.
$/phi$함수는 $x_i$에 대해 tree의 leaf node를 매핑해주는 함수인데, 트리는 비선형구조이며 미분이 불가능하기
때문에 다항함수의 합으로 근사하여 미분하는 것이다.

gradient와 hessian의 계산은 다음과 같다.
Loss function L을 F에 대하여 편미분한다.

이렇게 편미분된 식에 대해서 $g_i, h_i$로 치환하여 수식을 단순화 한다.

이때 남은 loss값은 이전의 예측값과 label을 비교하는 것이므로 상수값이다. (이전의 트리는 모두 결정되어 있는 상태)
우리는 미분을 통한 결과값이 필요하기 때문에 상수값을 제거하여 생각할 것이다.

이후 i와 j 값을 통일해주어야 하는데, 변수 $/tau$는 leaf node의 개수이기 때문에 j번째 leaf node $I_j$에 포함된 i값의
합을 통해 모든 수식을 j로 통일해줄 수 있다.

이후에 치환을 통해 수식을 정리하면 Loss function을 최소화 하는 x는 다음과 같아진다.

그리고 이렇게 구한 $w_j$의 최적화된 값을 원래의 objective function에 넣게 되면 Tree의 성능 지표로 사용할 수 있는
지표가 나오게 된다.
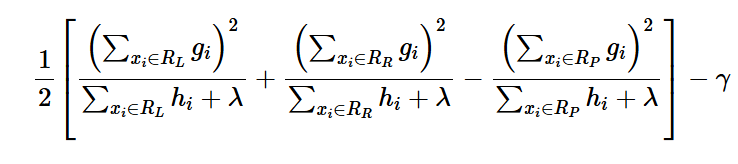
이 지표를 사용하여 트리의 분할 지점을 결정하는 것이다.
이 지표가 높다는 뜻이 무엇일까?
$R_L$은 Left node의 집합이고 $R_R$은 right node의 집합이다.
왼쪽과 오른쪽 노드의 지표 합에서 부모노드의 지표를 빼면 loss가 얼만큼 줄어들었는지에 대한 정보가 나오기 때문에
이를 최대화하는 분할 구간에서 트리를 나누는 것이다.
하지만 hessian의 계산에는 시간이 오래 걸리기 때문에 모든 포인트에 대한 지표를 계산할 수 없다.
(1) Global Variant
- 전체 데이터를 한꺼번에 고려해서, 전체적으로 손실을 가장 많이 줄일 수 있는 분할을 찾음.
- 하나의 feature 전체에 대해 최적의 분할값을 계산하고, 가장 이득(gain)이 큰 것을 선택.
- 일반적인 방식이며, 계산 비용이 높음.
- Gain 계산 시 전체 gradient와 hessian을 모두 합산해서 계산.
(2) Local Variant
- 하나의 노드 안에서만 국소적으로(local) 분할 기준을 계산함.
- 현재 노드의 데이터를 정렬해가며, 부분합을 갱신하면서 분할점을 빠르게 찾는 방식.
- 계산을 효율적으로 하고 싶을 때 사용.
- LightGBM이나 Histogram 방식에서 자주 사용됨.
이 두과정을 통해 split point를 찾는다고 한다.

그리고 tree에 대한 업데이트는 이번 시도에 만들어진 tree에 대해서 learning rate를 곱하여 이전 트리모형에 더해주는 방식을 사용한다.
-> 잔차 보완
'머신러닝 기초' 카테고리의 다른 글
| CatBoost (0) | 2025.05.17 |
|---|---|
| Lightgbm (0) | 2025.05.17 |
| Gradient Boosting Machines (GBM) (0) | 2025.05.16 |
| Adaptive Boosting (Ada Boosting) (0) | 2025.05.16 |
| RandomForest (2) | 2025.04.13 |





