Linear Regression

딥러닝의 기초가 부족하여 처음부터  기초를 탄탄히 쌓으려고 한다. 

 

고고~!

 

 

 

우선 Linear regression에 대해 배워보려고 한다. 

 

Linear: 그래프상에 표현되는 직선을 의미한다. 

 

Regression: variable들의 관계를 추정하기 위해 process를 분석하는 것을 의미한다. 

 

우리는 주어진 데이터를 이용하여 다음에 올 데이터의 값을 유추해야 한다. 

 

그랬을때 어떤 선형 방정식을 그려서 데이터의 값을 예측해야 할까?

 

 

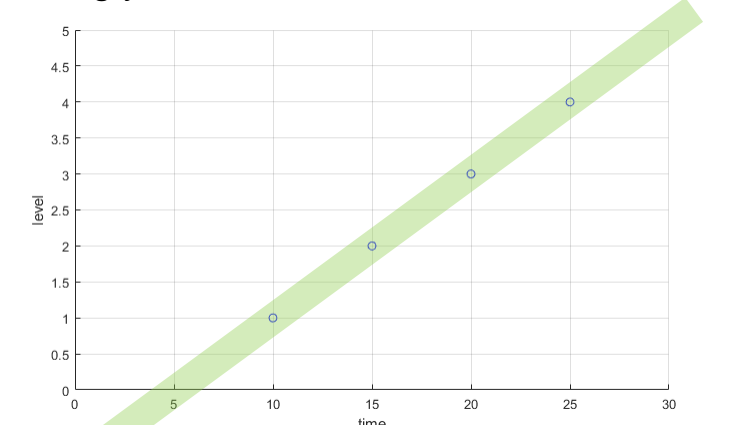
아마도 다음과 같은 그래프를 생각해볼 것이다. 

 

그렇다면 어떻게 이 그래프를 생각해낸 것일까?

 

 

이 세가지 선 중에서는 어떤 선이 데이터를 가장 잘 표현한 선일까?

 

A라고 생각할 것이다. 

 

 

그렇다면 A, B 중에서는 어떤 그래프가 더 데이터를 잘 표현한 선일까?

 

정말 애매하다. 

 

우리는 어떤 선이 데이터를 얼마나 잘 표현했는지를 정하는 구분방식을 만들 필요가 있다. 

 

우선 이 선의 수식을 다음과 같이 표현한다고 생각해보자. 

 

$H(x) =  Wx + b$

 

이때 W, b를 parameter라고 부를 것이고, x를 Variable이라고 부를 것이다. 

 

Variable은 고정된 상태로 존재한다고 가정하자. (데이터는 이미 주어진 상태)

 

우리가 바꿀 수 있는 것은 parameters 뿐이다. 

 

우리는 추정한 선이 얼마나 정확한지에 대한 지표를 정해야 한다. 

 

이 정확도를 표현하는 함수를 cost function 또는 loss function이라고 한다. 

 

 

우리는 Regression의 대표적인 cost function인 MSE 함수를 사용할 것이다. 

 

근데 왜 오차의 제곱을 사용할까? 

예측값보다 정답이 작을 때 -> 음수 

예측값보다 정답이 클 때 -> 양수 

 

만약 시그마를 사용하여 이 모든 오차를 합한다면 양수와 음수는 상쇄되어 오차가 왜곡되기 때문에 절댓값이나 제곱을 사용하는 것이다. 

 

이때 제곱을 사용하는 cost function을 Mean Squared Error라고 하고 절댓값을 사용하는 cost function을 Mean Absolute Error라고 한다. 

 

loss function을 정했다면 우리는 parameter를 어떤 방식으로 바꿔나갈지도 정해야한다. 

-> 마구잡이로 바꿀 수는 없기 때문

 

이때 모델의 Weight update는 Gradient Descent 방식을 사용한다. 

-> loss function을 weight로 편미분하여 기울기의 반대방향으로 weight를 조금씩 옮긴다. 

 

왜 기울기의 반대방향으로 옮기는 것일까? 

-> 블로그의 다음 포스팅으로 써봐야겠다. 

 

왜 조금씩 옮겨야 하는가?

 

 

-> 우리는 cost function의 현재위치 기울기의 반대방향으로 parameter들을 업데이트 하고 있다. 

 

하지만 기울기의 반대방향으로 업데이트한 parameter 값은 함수 위로 업데이트 하는 것이 아닌 함수값의 근사하여 parameter를 옮기는 것이다. 

 

정확히 말하자면 테일러 급수의 일차항만을 사용하여 cost function을 근사한다고 보면 될 것이다.

(이것도 다른 포스팅에 적을 예정)

 

그렇기 때문에 기울기의 반대방향으로 parameter들을 옮기는 것도 정도를 조절해야 한다. 

 

이 조절을 Learning rate($alpha$)로 조절을 하는데 너무 크게 조정을 한다면 초록색 선과 같이 극소점으로 수렴하지 못할 것이고

너무 작게 한다면 파란 선처럼 극소점까지 도달하지 못할 것이다. 

 

따라서 적절한( 빨간선) Learning rate값을 조정할 필요성이 있는 것이다. 

 

 

다음 글은 Logistic regression에 대해서 다룰 것이다.