[Data Structure] T tree

오늘 소개할 자료구조는 T tree입니다.

T 트리는 AVL 트리의 이진 탐색 특성 및 높이 균형과 B 트리의 업데이트, 저장효율 장점을 모두 취한 

MMDB(Main-Memory Database) 최적화 트리이다.

 

Background

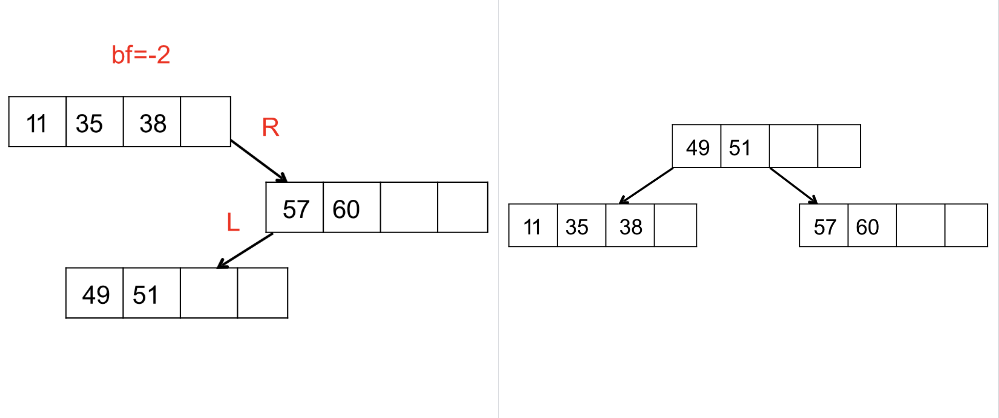
AVL 트리의 공간 낭비와 잦은 회전 연산을 개선하기 위해 만들어짐

AVL 트리가 하나의 노드에 데이터 한개만을 가지는 대신 T 트리는 하나의 노드가 n개의 데이터를

가질 수 있도록 개선한 구조임

 

장점

B트리의 엔트리가 해당 레코드를 포함하는 데이터 페이지를 가리키고 있는데 반해 T 트리의 각각의 엔트리가

해당 레코드의 메모리 주소를 직접 포인팅하고 있기 때문에 T트리 인덱스는 논리적 주소를 물리적 주소로 변환하는

작업 없이 원하는 레코드에 빠르게 접근할 수 있다.

T트리는 인덱스 노드에 키값을 포함하지 않고 직접 메모리 내의 레코드를 포인팅하기 때문에 메모리 사용량을

줄일 수 있다.

인덱스 전체가 메인 메모리에 상주하므로 디스크I/O를 하지 않는다.

알고리즘 자체가 매우 간단하여 코드 복잡성을 줄일 수 있음.

 

단점

1차원 데이터에만 적용 가능한 인덱스: 공간 데이터에 사용 불가

 

시간복잡도

O(log2[N/M]), N=전체 키의 개수, M=노드당 키의 개수

 

Search(탐색)

맨위의 노드를 p라고 하고 찾는 값을 v라고 하자

p노드의 최솟값 > v -> 왼쪽 서브트리 탐색

p노드의 최댓값 < v -> 오른쪽 서브트리 탐색

p 노드의 최솟값 < v < p 노드의 최댓값 -> 해당노드 탐색

 

 insert(삽입)

 

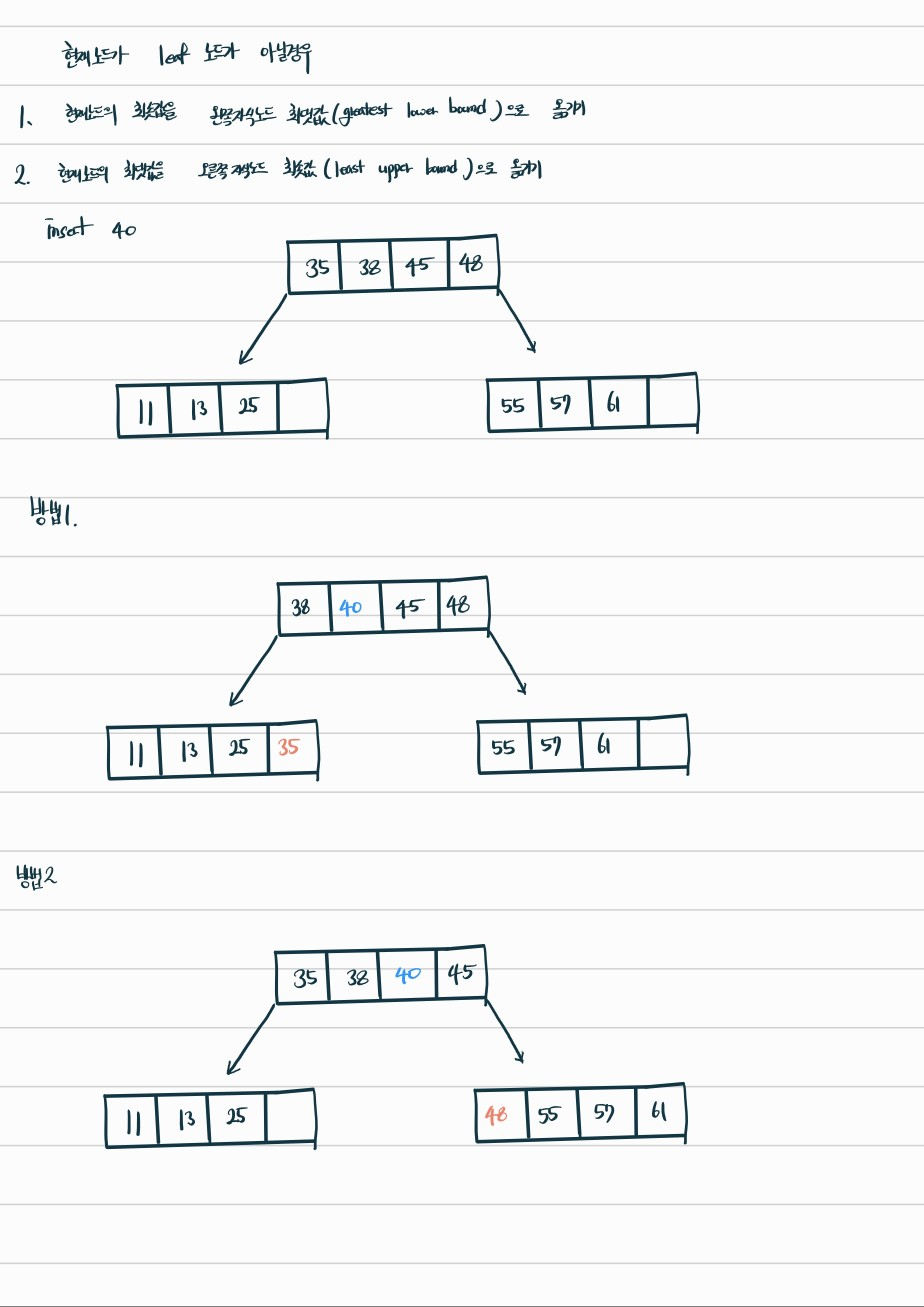
삽입하려는 노드가 leaf노드일 경우

삽입하려는 노드가 leaf 노드가 아닐경우

1. 현재노드의 최솟값을 왼쪽 자식노드 최댓값(greatest lower bound)로 옮기기

2. 현재노드의 최댓값을 오른쪽 자식노드 최솟값(least upper bound)로 옮기기

 

 

Delete( 삭제 )

 

Leaf Node Underflow

리프 노드가 N-1개의 데이터를 가질 경우 부모 노드와 합병해야 한다.

 

1. 루트 노드에서 부터 삭제할 키 x를 탐색한다

2. x를 찾으면 삭제

2-1. x가 리프노드에 있을 경우 부모노드와 합병한다.

2-2. x가 내부노드에 있을 경우 왼쪽 서브트리의 최대값을 부모노드로 옮기거나 오른쪽 서브트리의 최소값을

부모 노드로 옮긴다.

2-3. 트리의 균형이 깨질 경우 회전을 통해 균형을 맞춘다.